what other information do you need to prove the triangles congruent using sas congruence postulate
Related Pages
Congruent Triangles
More Geometry Lessons
Coinciding Triangles
Congruent triangles are triangles that take the aforementioned size and shape. This means that the respective sides are equal and the respective angles are equal.
We can tell whether ii triangles are congruent without testing all the sides and all the angles of the ii triangles. In this lesson, we will consider the four rules to bear witness triangle congruence. They are chosen the SSS rule, SAS rule, ASA dominion and AAS rule. In another lesson, we volition consider a proof used for right triangles chosen the Hypotenuse Leg rule. As long equally one of the rules is true, information technology is sufficient to prove that the two triangles are coinciding.
The following diagrams show the Rules for Triangle Congruency: SSS, SAS, ASA, AAS and RHS. Accept note that SSA is not sufficient for Triangle Congruency. Coil downwards the page for more examples, solutions and proofs.
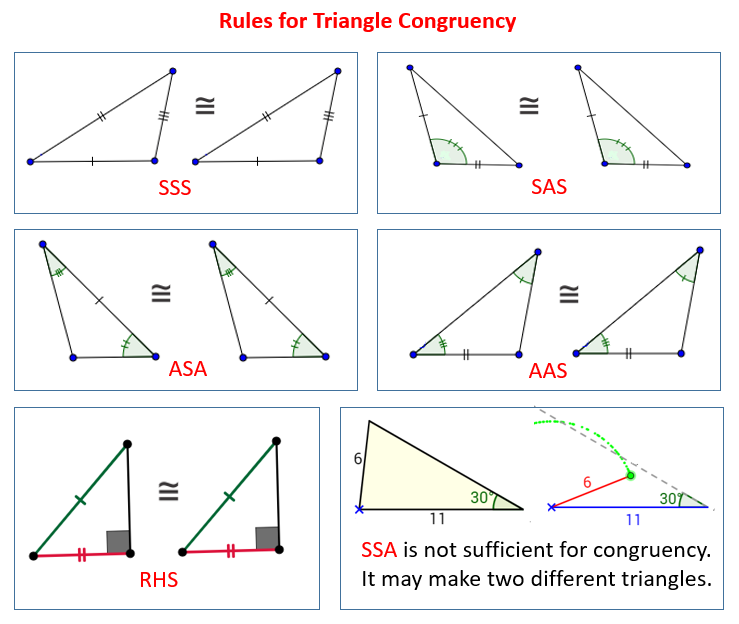
Side-Side-Side (SSS) Rule
Side-Side-Side is a rule used to prove whether a given set of triangles are coinciding.
The SSS rule states that:
If 3 sides of one triangle are equal to iii sides of another triangle, then the triangles are coinciding.
In the diagrams below, if AB = RP, BC = PQ and CA = QR, then triangle ABC is congruent to triangle RPQ.

Side-Angle-Side (SAS) Rule
Side-Angle-Side is a rule used to bear witness whether a given set of triangles are congruent.
The SAS rule states that:
If two sides and the included angle of one triangle are equal to two sides and included bending of some other triangle, then the triangles are congruent.
An included angle is an angle formed by two given sides.

Included Bending Not-included angle
For the 2 triangles below, if AC = PQ, BC = PR and angle C< = angle P, and then by the SAS rule, triangle ABC is congruent to triangle QRP.

Angle-Side-Angle (ASA) Rule
Angle-side-angle is a rule used to prove whether a given prepare of triangles are congruent.
The ASA dominion states that:
If two angles and the included side of one triangle are equal to two angles and included side of another triangle, then the triangles are coinciding.
Angle-Angle-Side (AAS) Rule
Angle-side-angle is a dominion used to prove whether a given set of triangles are congruent.
The AAS rule states that:
If two angles and a non-included side of 1 triangle are equal to two angles and a not-included side of another triangle, then the triangles are congruent.
In the diagrams below, if Air-conditioning = QP, angle A = angle Q, and angle B = angle R, then triangle ABC is congruent to triangle QRP.

Three Ways To Prove Triangles Congruent
A video lesson on SAS, ASA and SSS.
- SSS Postulate: If in that location exists a correspondence between the vertices of 2 triangles such that three sides of one triangle are coinciding to the respective sides of the other triangle, the two triangles are coinciding.
- SAS Postulate: If in that location exists a correspondence betwixt the vertices of two triangles such that the two sides and the included angle of ane triangle are congruent to the corresponding parts of the other triangle, the two triangles are congruent.
- ASA Postulate: If there exits a correspondence between the vertices of two triangles such that ii angles and the included side of 1 triangle are congruent to the corresponding parts of the other triangle, the 2 triangles are congruent.
- Prove Video Lesson
Using Ii Column Proofs To Prove Triangles Congruent
Triangle Congruence by SSS
How to Prove Triangles Congruent using the Side Side Side Postulate?
If three sides of one triangle are congruent to iii sides of another triangle, then the 2 triangles are congruent.
- Show Video Lesson
Triangle Congruence past SAS
How to Prove Triangles Coinciding using the SAS Postulate?
If two sides and the included bending of one triangle are congruent to two sides and the included angle of another triangle, then the two triangles are congruent.
- Show Video Lesson
Evidence Triangle Congruence with ASA Postulate
How to Show Triangles Congruent using the Angle Side Angle Postulate?
If 2 angles and the included side of ane triangle are coinciding to 2 angles and the included side of some other triangle, and so the ii triangles are congruent.
- Testify Video Lesson
Bear witness Triangle Congruence by AAS Postulate
How to Prove Triangles Congruent using the Angle Angle Side Postulate?
If two angles and a non-included side of one triangle are coinciding to ii angles and a not-included side of some other triangle, so the ii triangles are congruent.
- Show Video Lesson
Try the free Mathway figurer and trouble solver below to do various math topics. Try the given examples, or type in your own problem and bank check your answer with the step-past-footstep explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.
Source: https://www.onlinemathlearning.com/prove-triangles-congruent.html
0 Response to "what other information do you need to prove the triangles congruent using sas congruence postulate"
Post a Comment